Sommaire
Comment la rotation de la Terre est-elle représentée en mathématiques ?
La rotation de la Terre est un phénomène fascinant qui a captivé l’attention des scientifiques et des mathématiciens depuis des siècles. Comprendre cette rotation est essentiel non seulement pour la navigation, mais aussi pour la compréhension des cycles naturels qui régissent notre planète. Dans cet article, nous explorerons comment les mathématiques modélisent ce mouvement complexe.
La rotation terrestre : un mouvement circulaire
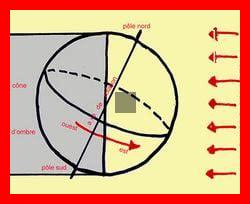
La Terre effectue une rotation complète sur elle-même en environ 24 heures, ce qui correspond à un mouvement circulaire. En mathématiques, ce mouvement peut être décrit à l’aide de concepts géométriques et trigonométriques. La Terre, considérée comme une sphère, tourne autour de son axe, qui est incliné d’environ 23,5 degrés par rapport au plan de son orbite autour du Soleil.
Pour représenter cette rotation, les mathématiciens utilisent des équations trigonométriques. Par exemple, la position d’un point sur la surface de la Terre peut être décrite en utilisant des coordonnées sphériques, où chaque point est défini par un angle de latitude et un angle de longitude. La formule de la position d’un point P sur la sphère peut être exprimée comme suit :
P(θ, φ) = (R * cos(θ) * cos(φ), R * cos(θ) * sin(φ), R * sin(θ))
où R est le rayon de la Terre, θ est la latitude et φ est la longitude.
Les effets de la rotation terrestre
La rotation de la Terre a également des conséquences importantes, telles que le phénomène de la force de Coriolis, qui influence les courants océaniques et les systèmes météorologiques. En mathématiques, cette force peut être modélisée par des équations différentielles qui prennent en compte la vitesse de rotation de la Terre et la position d’un objet en mouvement.
La force de Coriolis est donnée par la formule :
F_c = 2 * m * v * ω * sin(θ)
où m est la masse de l’objet, v est sa vitesse, ω est la vitesse angulaire de la Terre, et θ est la latitude. Cette équation montre comment la rotation de la Terre affecte le mouvement des objets en fonction de leur position géographique.
Conclusion
En somme, la rotation de la Terre est un sujet riche en implications mathématiques. Des modèles géométriques aux équations différentielles, les mathématiques offrent des outils puissants pour comprendre ce phénomène naturel. En explorant ces concepts, nous pouvons mieux appréhender non seulement la dynamique de notre planète, mais aussi les effets qu’elle a sur notre vie quotidienne.