Sommaire
Comment calculer le centre de gravité d’une forme géométrique
Le centre de gravité, également connu sous le nom de centre de masse, est un point crucial dans l’étude des formes géométriques. Il représente l’endroit où la masse d’un objet est concentrée et où il peut être équilibré. Dans cet article, nous allons explorer les méthodes pour calculer le centre de gravité de différentes formes géométriques.
Qu’est-ce que le centre de gravité ?
Le centre de gravité d’un objet est le point où la force de gravité peut être considérée comme agissant. Pour des formes symétriques comme un cercle ou un carré, le centre de gravité se trouve au centre de la forme. Cependant, pour des formes plus complexes, le calcul peut devenir plus délicat.
Calcul du centre de gravité pour des formes simples
Pour des formes géométriques simples, comme un rectangle ou un triangle, le calcul du centre de gravité est relativement simple. Par exemple, pour un rectangle, le centre de gravité se trouve à l’intersection des médianes. Si l’on considère un rectangle de largeur (L) et de hauteur (H), le centre de gravité se situe aux coordonnées ((L/2, H/2)).
Pour un triangle, le centre de gravité se trouve à un tiers de la hauteur à partir de la base. Si le triangle a une base de longueur (b) et une hauteur (h), le centre de gravité est situé aux coordonnées ((b/2, h/3)).
Calcul du centre de gravité pour des formes complexes
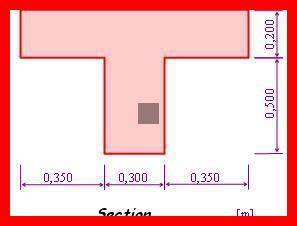
Pour des formes plus complexes, comme un polygone irrégulier ou une combinaison de plusieurs formes, la méthode de calcul devient plus élaborée. Une approche courante consiste à diviser la forme en plusieurs parties simples, calculer le centre de gravité de chaque partie, puis utiliser la formule de la moyenne pondérée.
La formule générale pour le centre de gravité ((x_{cg}, y_{cg})) d’une forme composée est donnée par :
xcg = (Σ(mi * xi)) / Σmi
ycg = (Σ(mi * yi)) / Σmi
où (m_i) est la masse de chaque partie et ((x_i, y_i)) sont les coordonnées de leur centre de gravité respectif.
Conclusion
Calculer le centre de gravité d’une forme géométrique est essentiel dans de nombreux domaines, notamment en ingénierie, en architecture et en physique. Que vous travailliez avec des formes simples ou complexes, comprendre les principes sous-jacents vous permettra d’appliquer ces concepts de manière efficace. En maîtrisant ces techniques, vous serez en mesure de résoudre des problèmes pratiques liés à l’équilibre et à la stabilité des objets.